Python Machine Learning VI - Master Gloomymoon's R2D2

Learning Best Practices for Model Evaluation and Hyperparameter Tuning

前面的课程我们学习了几种基本的机器学习分类算法，以及如何对数据进行预处理。本章将介绍通过调优获得更好的建模效果，以及如何评估模型的表现：

获取模型表现的无偏估计量
分析诊断机器学习算法中碰到的普遍问题
模型调优
通过各种指标评估预测效果

Streamlining workflows with pipelines

之前我们接触到的预处理技术，例如标准化、主成分分析，都会将训练获得参数服用到新的数据上，比如测试数据集。本节将介绍一个超级好用的工具，scikit-learn中的Pipeline类，支持训练模型中任意多次转换并在新数据集上进行预测。

Loading the Breast Cancer Wisconsin dataset
本章节我们将使用威斯康辛乳癌数据，包含569个样本。数据前两列包含记录的唯一识别号和对应的肿瘤类型（M=恶性，B=良性），3-32列包含了30个从细胞影响计算得出的实数型变量，我们将用着30个变量来建立一个预测良性恶性肿瘤的模型。首先从UCI网站上读取数据及，并拆分成训练和测试集：

import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data', eader=None)

from sklearn.preprocessing import LabelEncoder
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le = LabelEncoder()
y = le.fit_transform(y)

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = \
    train_test_split(X, y, test_size=0.20, random_state=1)

le.transform(['M', 'B'])

Output:

1	array([1, 0], dtype=int64)

简单的通过LabelEncoder类将目标分类从字符串转换为整型，1表示恶性，0表示良性。然后数据按照80:20的比例随机分为训练集和测试集。

Combining transformers and estimators in a pipeline
首先我们需要将数据标准化到同一尺度上，然后使用PCA将30维数据压缩到更低的二维子空间上。这次我们将StandardScaler、PCA、LogisticRegression对象全部串联到管道（pipeline）上处理：

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
pipe_lr = Pipeline([('scl', StandardScaler()),
                    ('pca', PCA(n_components=2)),
                    ('clf', LogisticRegression(random_state=1))])
pipe_lr.fit(X_train, y_train)
print('Test Accuracy: %.3f' % pipe_lr.score(X_test, y_test))

Output:

1	Test Accuracy: 0.947

Pipeline对象初始化时接受一个包含多个元祖的列表，元祖的第一个元素表示管道中每个对象的标识符，第二个元素是scikit-learn的转换器或算子。
管道对象的中间步骤作为转换器，最后一个步骤是算子。上述示例代码中创建了一个包含2个中间步骤和1个逻辑回归分类器的管道。当我们对管道对象pipe_lr实行fit操作室，中间步骤会执行fit和transform，并将结果数据传递给下一个步骤使用。管道工作的示意图如下：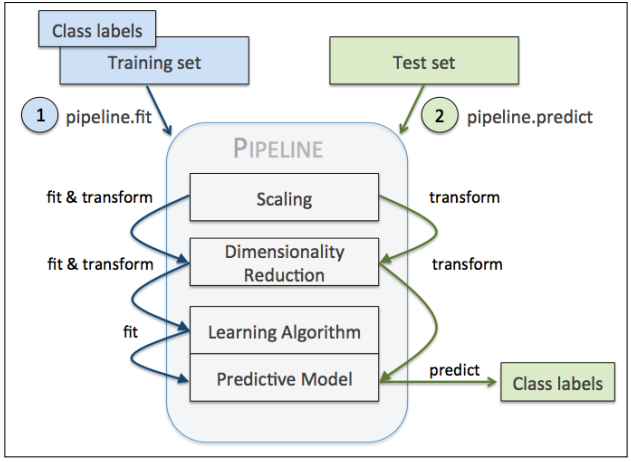

Using k-fold cross-validation to assess model performance

构建预测模型关键步骤之一就是评估模型在未知数据上的表现情况。如果我们在同一个数据集上开发和验证效果，会造成模型的欠拟合和过拟合问题。为了平衡偏置-方差（bias-variance），需要谨慎评估模型效果。这节将介绍的holdout交叉检验和k-fold交叉检验能够使我们获得可信的模型泛化误差，从而得知模型在未知数据上的表现好坏。

The holdout method
常规的建模方法是将原始数据分为训练集和测试集，前者用来训练模型，后者用来检验效果。通常为了提升模型的泛化能力我们会不断调整参数找到最优的模型，如果这是我们一直使用测试集来验证效果，那么测试数据会成为训练数据的一部分使模型产生过拟合。
更好的方法是将原始数据分为三份：训练集、验证集、测试集。使用验证集而不是测试集来做模型优化。下图是使用这种交叉检验方法的流程示意图，我们可以在验证集上不断验证和优化模型参数，优化完成后再在测试集上评估模型的泛化误差：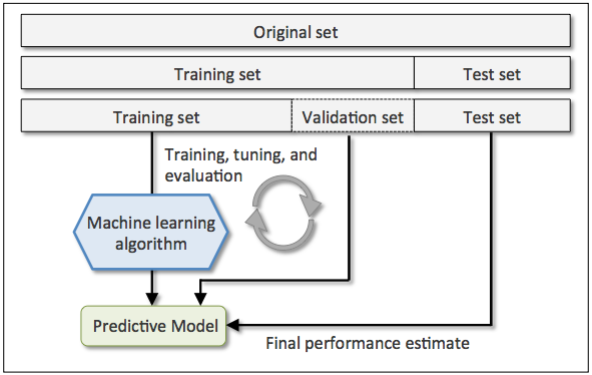

这样做的一个问题是评估会严重受到如何区分数据的影响，因此又产生了更加健壮的交叉检验方法：k-fold。

K-fold cross-validation
k-fold交叉检验的方法是，我们将训练数据随机分成k份（无放回抽样），k-1份用来建模，1份用来测试。这个过程重复k次，获得k个模型和对应的表现评估结果。其过程如下图：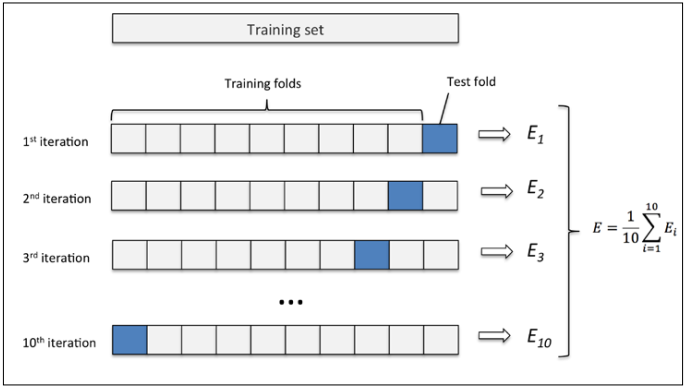

这里k=10，E表示模型的效果（例如分类准确度）。对于一般情况下，10是一个合理的数量，如果训练数据很小，可以适当提升这个数量。当我们提升k时，每次迭代都会用到更多的训练数据，结果是降低偏置（bias）。但是k过大也会增加计算时间，并且增加方差（variance），因为每次迭代的训练集都会非常相似。

当数据量非常小的情况下推荐使用特殊的交叉检验方法leave-one-out（LOO），在LOO中，k等于样本数n，这意味着每次迭代都只有一条记录用于测试。

在标准k-fold交叉检验基础上的一个小改进是分层（stratified）技术。在数据分fold的时候要保持分类标签的占比与原始数据中的占比一致。

import numpy as np
from sklearn.cross_validation import StratifiedKFold
kfold = StratifiedKFold(y=y_train, n_folds=10, random_state=1)
scores = []
for k, (train, test) in enumerate(kfold):
    pipe_lr.fit(X_train[train], y_train[train])
    score = pipe_lr.score(X_train[test], y_train[test])
    scores.append(score)
    print('Fold: %s, Class dist.: %s, Acc: %.3f' % (k+1, np.bincount(y_train[train]), score))

print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))

Output:

Fold: 1, Class dist.: [256 153], Acc: 0.891
Fold: 2, Class dist.: [256 153], Acc: 0.978
Fold: 3, Class dist.: [256 153], Acc: 0.978
Fold: 4, Class dist.: [256 153], Acc: 0.913
Fold: 5, Class dist.: [256 153], Acc: 0.935
Fold: 6, Class dist.: [257 153], Acc: 0.978
Fold: 7, Class dist.: [257 153], Acc: 0.933
Fold: 8, Class dist.: [257 153], Acc: 0.956
Fold: 9, Class dist.: [257 153], Acc: 0.978
Fold: 10, Class dist.: [257 153], Acc: 0.956

CV accuracy: 0.950 +/- 0.029

首先我们按照y_train数据为分类标签初始化一个StratifiedKFold迭代器，然后进行k次迭代，每次使用train下标数组筛选出训练集，并提供到之前我们定义的pile_lr管道中，并使用test下标数组筛选出的测试集计算准确度，并收集到scores列表中，最后计算平均准确度和标准差。
scikit-learn提供了更加方便的评分类，能够直接使用分层k-fold交叉检验得到模型的效果：

from sklearn.cross_validation import cross_val_score
scores = cross_val_score(estimator=pipe_lr,
                         X=X_train,
                         y=y_train,
                         cv=10,
                         n_jobs=1)
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))

Output一样。
cross_val_score另一个有用的特性是可以利用多个CPU分布执行，如果将n_jobs参数设置为2，就可以使用2个CPU执行10次迭代，如果设置为-1，则可以使用所有的可用CPU。

Debugging algorithms with learning and validation curves

本节将介绍两个简单但是强大的分析工具能够帮助我们提升预测模型的性能：学习曲线（learning curves）和验证曲线（validation curves）。

Diagnosing bias and variance problems with learning curves
如果预测模型构建的过于复杂，会在训练数据上过拟合，从而失去对未知数据的泛化能力。通常收集更多的训练样本有助于降低过拟合，但是在实际中者往往困难重重。通过绘制不同大小训练集下模型的训练和验证的准确度曲线，可以非常容易地检测出模型是否存在偏差或方差，以及更多的数据是否有助于解决问题。在绘制学习曲线和验证曲线前，我们先来看下偏差和方差问题的例子。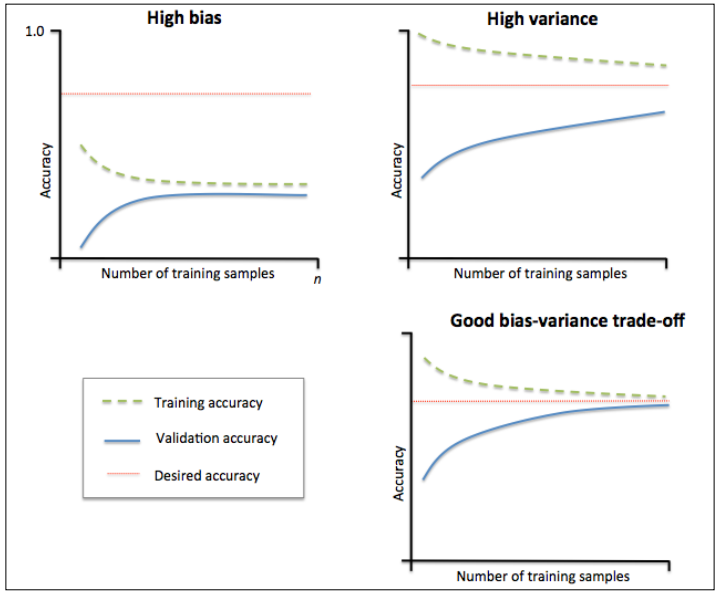

左上图的模型表现为高偏差（high bias），训练准确度和交叉验证准确度都较低，意味着模型欠拟合。常用的解决方案是增加模型的参数数量，或降低正则化力度。
有上图的模型表现为高方差（high variance），表现为训练准确度和交叉验证准确度之间巨大的差异，意味着模型在训练数据集上过拟合。常用的解决方案是增加训练数据，降低模型复杂程度，对于非正则化模型也可以利用特征选择和特征压缩的技术降低特征数量。

首先我们使用scikit-learn中的学习曲线功能评估模型：

import matplotlib.pyplot as plt
from sklearn.learning_curve import learning_curve
pipe_lr = Pipeline([
                    ('scl', StandardScaler()),
                    ('clf', LogisticRegression(penalty='l2', random_state=0))])
train_sizes, train_scores, test_scores = \
    learning_curve(estimator=pipe_lr,
                   X=X_train,
                   y=y_train,
                   train_sizes=np.linspace(0.1, 1.0, 10),
                   cv=10,
                   n_jobs=1)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(train_sizes, train_mean, color='blue', 
         marker='o', markersize=5, label='training accuracy')
plt.fill_between(train_sizes, train_mean + train_std, train_mean - train_std, 
                 alpha=0.15, color='blue')
plt.plot(train_sizes, test_mean, color='green', linestyle='--',
         marker='s', markersize=5,
         label='validation accuracy')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, 
                 alpha=0.15, color='green')
plt.grid()
plt.xlabel('Number of training samples')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.8, 1.0])
plt.show()

Output: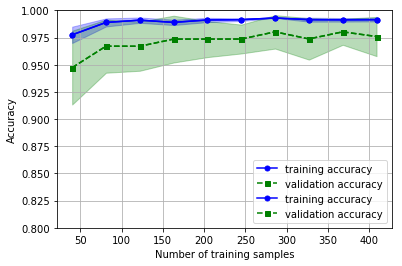

通过设置learning_curve方法的train_sizes参数，可以控制用来生成学习曲线的样本数据的相对数量或绝对数量，这里我们使用np.linspace(0.1, 1.0, 10)生成10分等差数来设置训练集的大小。默认情况下learning_curve方法是用分层k-fold交叉检验，通过cv参数设置k为10。最后我们简单计算交叉检验后的平均训练和测试精准度，并用plot方法展现，并用fill_between方法绘制平均精准度的标准差。

从图中可以看出，模型在测试集上的表现还不错，但是有轻微的过拟合，训练和验证精准度之间存在一定的差距。

Addressing overfitting and underfitting with validation curves
验证曲线可以定位过拟合或欠拟合问题从而有效帮助提升模型性能。和学习曲线不同，验证曲线描绘的是基于不同模型参数情况下训练和验证精准度情况，本示例中逻辑回归的参数是C。

from sklearn.learning_curve import validation_curve
param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
train_scores, test_scores = validation_curve(
                estimator=pipe_lr,
                X=X_train,
                y=y_train,
                param_name='clf__C',
                param_range=param_range,
                cv=10)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(param_range, train_mean, color='blue', 
         marker='o', markersize=5, label='training accuracy')
plt.fill_between(param_range, train_mean + train_std, train_mean - train_std, 
                 alpha=0.15, color='blue')
plt.plot(param_range, test_mean, color='green', linestyle='--',
         marker='s', markersize=5,
         label='validation accuracy')
plt.fill_between(param_range, test_mean + test_std, test_mean - test_std, 
                 alpha=0.15, color='green')
plt.grid()
plt.xscale('log')
plt.xlabel('Parameter C')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.8, 1.0])
plt.show()

Output: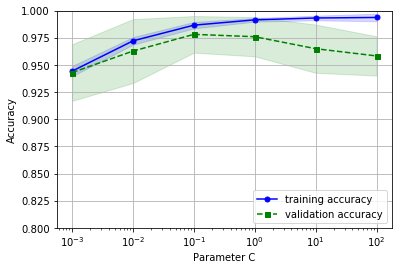

类似学习曲线方法，validation_curve方法默认使用分层k-fold交叉检验，通过param_name参数设置我们希望评估的模型参数，本例子中，通过'clf__C'来访问管道中LogisticRegression分类器对象的参数C，param_range用于指定参数的取值范围。最后绘制平均准确度和标准差图像。

从结果可以发现，当C变小（加强正则化）时，模型出现轻微欠拟合，而C增大时模型又出现过拟合，参数C的甜区大约在0.1左右。

Fine-tuning machine learning models via grid search

在机器学习算法中，有两类参数：通过训练数据学习道德参数，例如逻辑回归中的权重，和算法优化的参数。后者是可调参数，也成为超参数（hyperparameters），例如逻辑回归中的正则化参数、决策树中的深度。

上节我们通过验证曲线调优一个超参数，本节将介绍一个更强大的超参数优化方法：网格搜索法（grid search），它能找到多个超参数的最优组合。

Tuning hyperparameters via grid search
网格搜索原理很简单，通过贪心算法评估我们给出的所有超参数组合来找到最优解：

from sklearn.grid_search import GridSearchCV
from sklearn.svm import SVC
pipe_svc = Pipeline([('scl', StandardScaler()),
                    ('clf', SVC(random_state=1))])
param_range = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]
param_grid = [{'clf__C': param_range,
               'clf__kernel': ['linear']},
              {'clf__C': param_range,
               'clf__gamma': param_range,
               'clf__kernel': ['rbf']}]
gs = GridSearchCV(estimator=pipe_svc,
                  param_grid=param_grid,
                  scoring='accuracy',
                  cv=10,
                  n_jobs=-1)
gs = gs.fit(X_train, y_train)
print(gs.best_score_, gs.best_params_)

Output:

1	0.978021978021978 {'clf__C': 0.1, 'clf__kernel': 'linear'}

上述代码中，我们创建一个GridSearchCV对象用来训练和调优一个支持向量机管道。param_grid参数定义一个包含多个字典的列表，存放了我们希望尝试的参数。对于线性SVM，只需要调试参数C，而对RBF核支持向量机，我们尝试参数C和gamma两个参数组合（gamma参数仅针对核支持向量机有效）。网络搜索完成后，可以从best_score_变量获取到最好模型的分数，best_params_变量获取对应的参数组合。本例中C=0.01时的线性SVM模型准确度最高，为97.8。

最后我们可以使用独立的测试数据集来评估最优模型的性能，可以通过best_estimator_属性获得。

1
2
3

clf = gs.best_estimator_
clf.fit(X_train, y_train)
print('Test accuracy: %.3f' % clf.score(X_test, y_test))

Output:

1	Test accuracy: 0.965

Algorithm selection with nested cross-validation
如果需要在不同的模型算法间调试比较，另一个推荐的方法是嵌套交叉检验（nested cross-validation）。其原理如下图，首先在外层是一个k-fold的交叉检验循环，将数据分为训练集和测试集，内层是另一个k-fold交叉检验用来做模型选择。图示中是一个外五内二的模型，这种典型的配置也成为5x2交叉检验。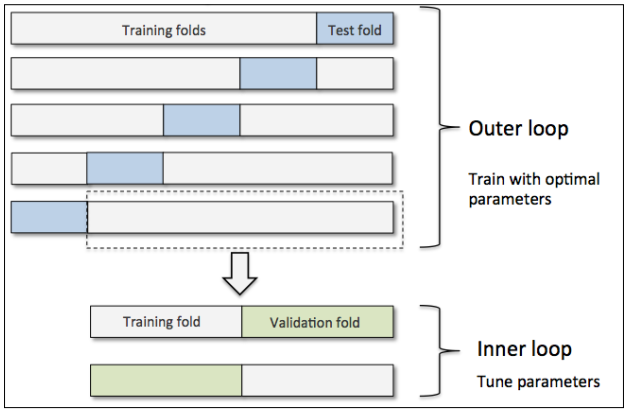

gs = GridSearchCV(estimator=pipe_svc,
                  param_grid=param_grid,
                  scoring='accuracy',
                  cv=10,
                  n_jobs=-1)
scores = cross_val_score(gs, X, y, scoring='accuracy', cv=5)
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))

Output:

1	CV accuracy: 0.972 +/- 0.012

同样我们可以用嵌套交叉检验比较决策树分类器，为了简化起见，这里仅仅调试深度参数：

from sklearn.tree import DecisionTreeClassifier
gs = GridSearchCV(estimator=DecisionTreeClassifier(random_state=0),
                  param_grid=[{'max_depth': [1, 2, 3, 4, 5, 6, 7, None]}],
                  scoring='accuracy',
                  cv=5)
scores = cross_val_score(gs,
                         X_train,
                         y_train,
                         scoring='accuracy',
                         cv=5)
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))

Output:

1	CV accuracy: 0.908 +/- 0.045

在这个例子上，SVM模型的表现显著优于决策树。

Looking at different performance evaluation metrics

前面的章节和段落，我们都是使用预测准确度来评估模型的效果，通常这是一个有用的指标。此外，还有不少指标也能够用于评估模型的效果，例如精确率（precision）、召回率（recall）和F1评分（F1-score）。

Reading a confusion matrix
首先需要介绍下混淆矩阵（confusion matrix），一个简单的展示真正（true positive）、真负（true negative）、假正（false postive）和假负（false negtive）数量的方阵，如下图所示：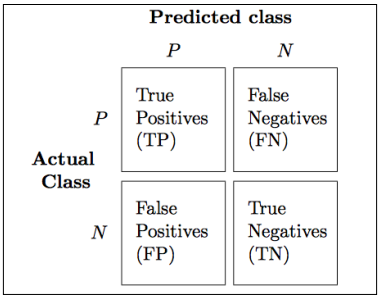

这些指标可以简单的根据预测结果计算出，scikit-learn也同时提供方便的confusion_matrix函数供我们直接使用：

from sklearn.metrics import confusion_matrix
pipe_svc.fit(X_train, y_train)
y_pred = pipe_svc.predict(X_test)
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(confmat)

Output:

1 2	[[71 1] [ 2 40]]

我们使用matplotlib的matshow函数来画一张类似上面的二维图表：

fig, ax = plt.subplots(figsize=(2.5, 2.5))
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
    for j in range(confmat.shape[1]):
        ax.text(x=j, y=i, s=confmat[i, j], va='center', ha='center')
plt.xlabel('predicted label')
plt.ylabel('true label')
plt.show()

Output: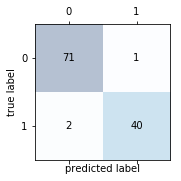

Optimizing the precision and recall of a classification model
预测错误（ERR）和准确（ACC）是衡量样本误分类的指标，ERR是所有错误分类数量除以预测总数，ACC是所有预测正确的数量除以预测总数。ACC=1-ERR。

真正率（TPR）和假正率（FPR）是衡量错无分类情况的指标，FPR=FP/(FP+TN)，TPR=TP/(FN+TP)。
在实际业务中，真正率和假正率可能是我们需要特别关注的，例如癌症检测中，对于恶性肿瘤的正确识别非常重要。

精准率（PRE）和召回（REC）是衡量真正和真负的指标，实际上召回率等同于真正率：PRE=TP/(TP+FP)，REC=TP/(FN+TP)。

实际中，会使用F1评分，它是精准率和召回率的组合形式：F1=2(PREREC)/(PRE+REC)。

上述这些评分指标都在sklearn.metrics模块中实现。

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score, f1_score
print('Precision: %.3f' % precision_score(y_true=y_test, y_pred=y_pred))

print('Recall: %.3f' % recall_score(y_true=y_test, y_pred=y_pred))

print('F1: %.3f' % f1_score(y_true=y_test, y_pred=y_pred))

Output:

Precision: 0.976

Recall: 0.952

F1: 0.964

通过GridSearch还有很多其他评价指标，访问详细列表。

注：scikit-learn中对于标记为1的分类视为正（positive）。

Plotting a receiver operating characteristic
受试者工作特征曲线（receiver operating characteristic，ROC），又称为感受性曲线，通过设置分类器不同的决策临界值，计算出一系列以假负率和真正率为坐标的性能曲线。基于ROC曲线，可以计算曲线下面积（area under then curve，AUC）来表示分类模型的性能。

下面我们将使用之前定义的逻辑回归管道，基于2个特征构建的分类器绘制ROC曲线，为了让图像更加直观，我们将StratifiedKFold的验证次数降低到三次。

from sklearn.metrics import roc_curve, auc
from scipy import interp
X_train2 = X_train[:, [4, 14]]
cv = StratifiedKFold(y_train, n_folds=3, random_state=1)
fig = plt.figure(figsize=(7, 5))
mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
all_tpr = []

for i, (train, test) in enumerate(cv):
    probas = pipe_lr.fit(X_train2[train],y_train[train]).predict_proba(X_train2[test])
    fpr, tpr, thresholds = roc_curve(y_train[test], probas[:, 1], pos_label=1)
    mean_tpr += interp(mean_fpr, fpr, tpr)
    mean_tpr[0] = 0.0
    roc_auc = auc(fpr, tpr)
    plt.plot(fpr, tpr, lw=1, label='ROC fold %d (area = %0.2f)' % (i+1, roc_auc))
plt.plot([0, 1], [0, 1], linestyle='--', color=(0.6, 0.6, 0.6),
         label='random guessing')
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--', label='mean ROC (area = %0.2f)' % mean_auc, lw=2)
plt.plot([0, 0, 1], [0, 1, 1], lw=2, linestyle=':', color='black', 
         label='perfect performance')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.title('Receiver Operator Characteristic')
plt.legend(loc='lower right')
plt.show()

Output: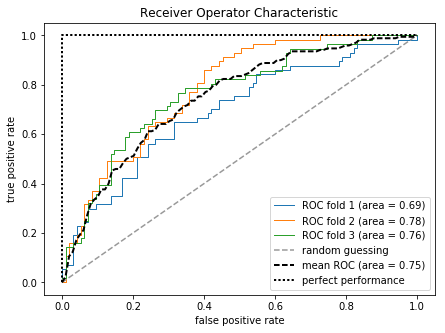

上述结果可以看出三次fold间存在一定的方差，平均ROC AUC为0.75。
如果我们仅仅关系ROC AUC分数，可以直接使用sklearn.metrics子模块的roc_auc_score方法。

pipe_svc = pipe_svc.fit(X_train2, y_train)
y_pred2 = pipe_svc.predict(X_test[:, [4, 14]])
from sklearn.metrics import roc_auc_score, accuracy_score
print('ROC AUC: %.3f' % roc_auc_score(y_true=y_test, y_score=y_pred2))

print('Accuracy: %.3f' % accuracy_score(y_true=y_test, y_pred=y_pred2))

Output:

1
2
3

ROC AUC: 0.671

Accuracy: 0.728

通过ROC AUC描述分类器的表现能够洞察模型在不平衡样本上的性能。

The scoring metrics for multiclass classification
暂略

Learning Best Practices for Model Evaluation and Hyperparameter Tuning

Streamlining workflows with pipelines

Using k-fold cross-validation to assess model performance

Debugging algorithms with learning and validation curves

Fine-tuning machine learning models via grid search

Looking at different performance evaluation metrics

FEATURED TAGS