5 Compressing Data via Dimensionality Reduction
本章将介绍三类基础方法,将训练数据映射到低维特征子空间。数据压缩是机器学习中一个重要的课题,它帮助我们存储和分析现代科技收集的增长惊人的数据。本章将涵盖如下主要内容:
- 主成分分析(Principal component analysis,PCA),用于无监督数据压缩
- 线性判别分析(Linear Discriminant Analysis,LDA),作为一种有监督的降维技术最大化区分性
- 利用核主成分分析法进行非线性降维
Unsupervised dimensionality reduction via principal component analysis
主成分分析(PCA)是一种无监督线性转换技术了,除了维度压缩以外也应用于很多其他领域,例如数据的探索分析、股票交易的信号降噪和生物信息学中的基因组数据分析及基因显性水平。PCA协助我们基于特征间的相关性识别数据中隐含的模式。简言之,PCA旨在找到高维数据中最大方差(variance)的方向并投射到一个有同等或更低维度的子空间上。新子空间中两两正交的轴(也就是主成份principal components)既可以视为方差最大的方向。如下图所示,x1和x2是原始的特征坐标,PC1和PC2即是主成份。子空间的维度是全新构造出来的的正交特征,也称为主元,而不是简单的从原始特征维中去除。PCA的算法原理这里不做介绍了。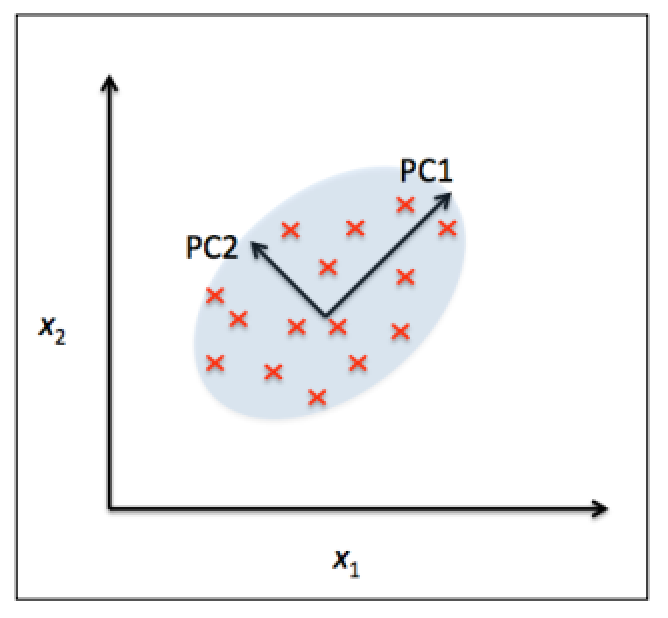
PCA算法主要步骤如下:
- 标准化d维的原始数据集
- 构建协方差矩阵
- 求解协方差矩阵的特征值(eigenvalues)和特征向量(eigenvactors)
- 取最大的k个特征值对应的特征向量
- 将选取的特征向量作为列向量组成投影矩阵w
- 使用w将样本数据投影到选取的k个特征向量上
Total and explained variance
本节我们先对付PCA算法的前四布:标准化数据、构建协方差矩阵、计算特征值和特征向量、排序特征向量。
我们仍使用上一张用到的Wine数据集来举例,并按照70:30的比例分为训练和测试集,然后进行方差为1的标准化。1
2
3
4
5
6
7
8
9import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import StandardScaler
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
Xtest_std = sc.fit_transform(X_test)
第二步是构建一个dxd维的协方差矩阵,d等于数据集中变量的个数,存放两两特征间的协方差,协方差值为正时表示两个变量同时增加后减少,负值表示变量变化趋势相反。我们可以直接使用NumPy中的linalg.eig函数直接计算Wine数据的协方差矩阵:1
2
3
4import numpy as np
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\nEigenvalues \n%s' % eigen_vals)
Output:1
2
3
4Eigenvalues
[ 4.8923083 2.46635032 1.42809973 1.01233462 0.84906459 0.60181514
0.52251546 0.08414846 0.33051429 0.29595018 0.16831254 0.21432212
0.2399553 ]
numpy.cov方法用于计算标准化后训练数据集的协方差矩阵,linalg.eig方法对协方差矩阵进行特征分解,返回一个含有13个特征值的响亮(eigen_vals)和对应的特征向量(存储为13x13维度的矩阵eigen_vecs)。因为我们希望通过引射到一个新的子空间上达到降低数据维度的目的,因此需要选择包含有最大信息的特征向量(也就是主成份),而特征值就定义了特征向量的重要程度,因此只要将特征值降序排列,提取我们感兴趣的前k个特征向量即可。在这之前我们先来看下每个特征值都赢得方差百分比(variance explained ratios)。每个特征值对应的方差百分比是其自身与所有特征值总和的比值。1
2
3
4
5
6
7
8
9
10tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', label='individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid', label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.show()
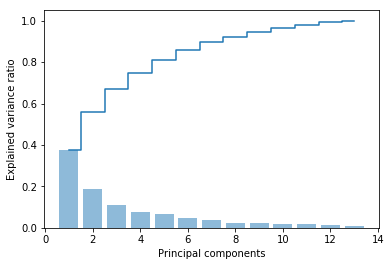
从结果上看,第一个主成份贡献了近40%的方差,前两个贡献了近60%的方差。
虽然方差解释图和上章中通过随机森林的特征选择类似,但是主成分分析是一种无监督的方法,其分析并不基于分类标签,而是衡量在特征轴上数据值的离散情况。
Feature transformation
完成协方差矩阵分写后就可以将Wine数据集转换到新的主成份特征向量上。首先是按照特征值降序对特征对排序:1
2
3eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
for i in range(len(eigen_vals))]
eigen_pairs.sort(reverse=True)
然后我们选取值最大的两个特征向量创建映射矩阵。因为为了展示方便,仅选取两个特征变量以便能够在二维散点图上展现,实际工作中主成份的数量需要衡量,综合考虑计算效率和分类器的效果。1
2
3w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis]))
print('Matrix W:\n', w)
Output:1
2
3
4
5
6
7
8
9
10
11
12
13
14Matrix W:
[[ 0.14669811 0.50417079]
[-0.24224554 0.24216889]
[-0.02993442 0.28698484]
[-0.25519002 -0.06468718]
[ 0.12079772 0.22995385]
[ 0.38934455 0.09363991]
[ 0.42326486 0.01088622]
[-0.30634956 0.01870216]
[ 0.30572219 0.03040352]
[-0.09869191 0.54527081]
[ 0.30032535 -0.27924322]
[ 0.36821154 -0.174365 ]
[ 0.29259713 0.36315461]]
在原始数据上对每一条记录进行转换(点积)就能够转换成2个新的特征,同样对所有数据应用映射也可以直接通过点积操作。最后我们通过二维散点图看下转换今后的数据分布情况。1
2
3
4
5
6
7
8
9
10
11X_train_pca = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train==l, 0],
X_train_pca[y_train==l, 1],
c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()
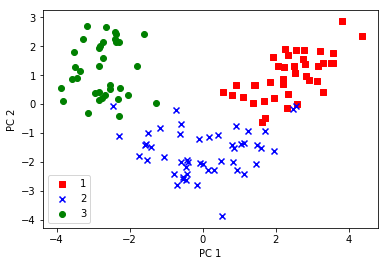
转换后的数据在X轴(第一个主成份)上的分布比Y轴(第二个主成份)上区分度更好,通过一个简单的线性分类器就能够很好地定义数据分布界限。
Principal component analysis in scikit-learn
scikit-learn中已经实现的PCA类是一个数据变化模块,和之前的类似,优先使用fit方法在训练数据上学习,然后转换训练数据和测试数据。下面我们结合PCA的转换、逻辑回归分类建模,并将模型结果用第二章中的方法展现出来:1
2
3
4
5
6
7
8
9
10
11
12
13from plot_decision_regions import *
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
lr = LogisticRegression()
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()
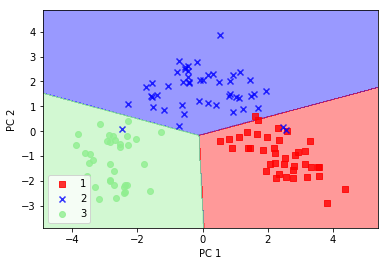
注意到这个散点图和我们自己实现的PCA不同,是X轴的镜像,这不是算法的错误,而是因为特征向量可正可负,我们可以简单的对数据乘以-1,使得结果一样。最后我们将逻辑归回模型应用在转换后的测试集上看下分类效果:1
2
3
4
5plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()
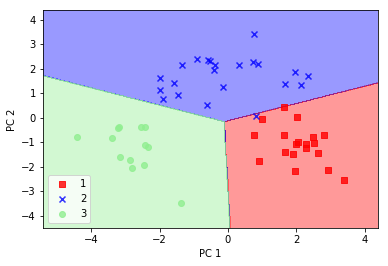
简单的逻辑回归在这个2维的特征子空间上表现不错,仅有1个样本被错误分类。
如果我们需要了解不同主成份的方差比例,可以在初始化PCA类的时候将参数n_components设置为None,这样所有的主成份都会保留,方差比例可以通过explained_variance_ratio_属性访问。1
2
3pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_
Output:1
2
3array([ 0.37329648, 0.18818926, 0.10896791, 0.07724389, 0.06478595,
0.04592014, 0.03986936, 0.02521914, 0.02258181, 0.01830924,
0.01635336, 0.01284271, 0.00642076])
Supervised data compression via linear discriminant analysis
线性判别分析(Linear Discriminant Analysis,LDA)是一种特征压缩技术,可以提升模型计算效率降低过拟合。和PCA背后的原理类似,LDA的目标是搜索一个分类分布更优的特征子空间。PCA和LDA都是通过线性转换技术降低数据的维度,前者是无监督算法,而后者是有监督的。直觉上有监督学习效果优于无监督学习,但是实际上在某些领域例如特定图像识别问题上,PCA反而有更加出色的表现。
LDA的主要步骤如下:
- 标准化d维数据(d表示特征的数量)
- 为每个分类计算d维的均值向量(mean vector)
- 构建类间散布矩阵Sb(between-class scatter matrix)和类内散布矩阵Sw(within-class scatter matrix)
- 计算(Sw^-1)(Sb)的特征向量和特征值
- 选择k个最大特征值对应的特征向量,组成d×k维的转换矩阵W,特征向量是矩阵的列
- 将样本通过W投射到新的特征子空间上
Computing the scatter matrices
因为在之前PCA步骤中我们已经标准化了Wine数据集,这里不再重复。我们首先为每个分类计算均值向量:1
2
3
4
5
6np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1, 4):
mean_vecs.append(np.mean(
X_train_std[y_train==label], axis=0))
print('MV %s: %s\n' %(label, mean_vecs[label-1]))
Output:1
2
3
4
5
6
7
8MV 1: [ 0.9259 -0.3091 0.2592 -0.7989 0.3039 0.9608 1.0515 -0.6306 0.5354
0.2209 0.4855 0.798 1.2017]
MV 2: [-0.8727 -0.3854 -0.4437 0.2481 -0.2409 -0.1059 0.0187 -0.0164 0.1095
-0.8796 0.4392 0.2776 -0.7016]
MV 3: [ 0.1637 0.8929 0.3249 0.5658 -0.01 -0.9499 -1.228 0.7436 -0.7652
0.979 -1.1698 -1.3007 -0.3912]
有了均值向量后我们可以用来计算类内散步矩阵Sw: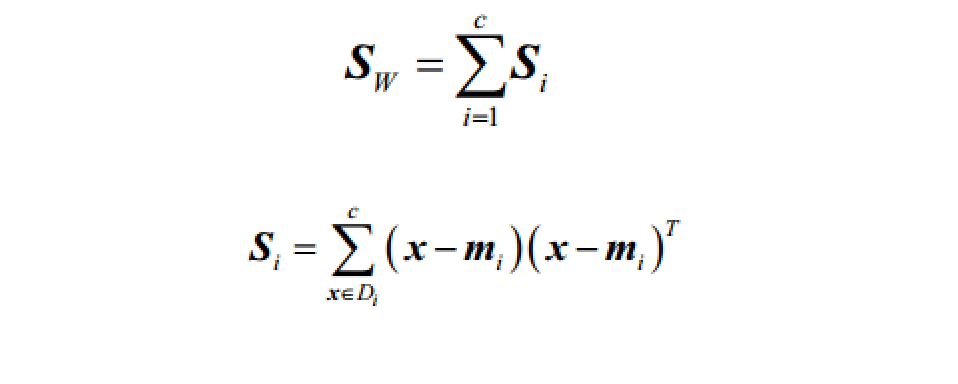
其中i代表分类,m是分类的均值向量,x是特征。1
2
3
4
5
6
7
8
9d = 13 # number of features
S_W = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter = np.zeros((d, d))
for row in X[y == label]:
row, mv = row.reshape(d, 1), mv.reshape(d, 1)
class_scatter += (row-mv).dot((row-mv).T)
S_W += class_scatter
print('Within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))
Output:1
Within-class scatter matrix: 13x13
由于我们在构建散步矩阵前假设训练集中的每个分类数量是均匀分布的,但是实际情况中,不可能这样完美:1
print('Class label distribution: %s' % np.bincount(y_train)[1:])
Output:1
Class label distribution: [40 49 35]
因此我们在汇总所有Si前需要做归一化处理,对每个Si都要除以分类i中样本的个数,这样有点类似于我们之前的协方差矩阵:1
2
3
4
5
6d = 13 # number of features
S_W = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter = np.cov(X_train_std[y_train==label].T)
S_W += class_scatter
print('Within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))
然后可以构建类间散布矩阵Sb: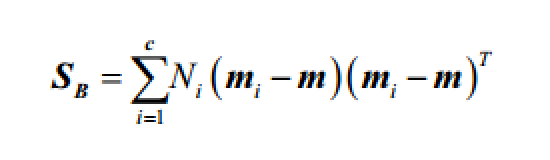
其中m是总体的均值向量。1
2
3
4
5
6
7
8
9mean_overall = np.mean(X_train_std, axis=0)
d = 13 # number of features
S_B = np.zeros((d, d))
for i, mean_vec in enumerate(mean_vecs):
n = X[y==i+1, :].shape[0]
mean_vec = mean_vec.reshape(d, 1)
mean_overall = mean_overall.reshape(d, 1)
S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
print('Between-class scatter matrix: %sx%s' % (S_B.shape[0], S_B.shape[1]))
Selecting linear discrimnants for the new feature subspace
接下来的工作与PCA类似:1
2
3
4
5
6
7eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
print('EigenValues in decreasing order:\n')
for eigen_val in eigen_pairs:
print(eigen_val[0])
`
降序排列的特征值如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15EigenValues in decreasing order:
643.015384346
225.086981854
8.00267518379e-14
5.75753461418e-14
3.51050796047e-14
3.46389583683e-14
2.58781151001e-14
2.58781151001e-14
2.44498173106e-14
1.65321991297e-14
8.33122517135e-15
2.3238388797e-15
6.52243007612e-16
熟悉线性代数的同学或许还记得一个d×d维的协方差矩阵的秩的数量不会超过d-1个,这里可以看到仅有两个非零的特征值。
我们同样用类似PCA中方差百分比的贡献度,将片别分析中每个分类判别的信息都通过图表来展现:1
2
3
4
5
6
7
8
9
10tot = sum(eigen_vals.real)
discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr = np.cumsum(discr)
plt.bar(range(1, 14), discr, alpha=0.5, align='center', label='individual "discriminability"')
plt.step(range(1, 14), cum_discr, where='mid', label='cumulative "discriminability"')
plt.ylabel('"discriminability" ratio')
plt.xlabel('Linear Discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.show()
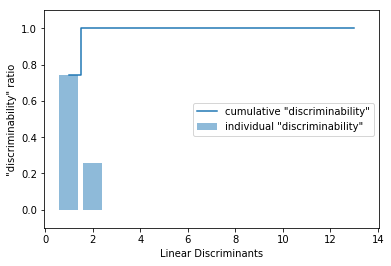
前两个线性判别式捕获了将近100%的有用分类信息。然后我们可以用这两个特征变量来组建转换矩阵W:1
2
3w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
eigen_pairs[1][1][:, np.newaxis].real))
print('Matrix W:\n', w)
Output:1
2
3
4
5
6
7
8
9
10
11
12
13
14Matrix W:
[[-0.0707 0.3778]
[ 0.0359 0.2223]
[-0.0263 0.3813]
[ 0.1875 -0.2955]
[-0.0033 -0.0143]
[ 0.2328 -0.0151]
[-0.7719 -0.2149]
[-0.0803 -0.0726]
[ 0.0896 -0.1767]
[ 0.1815 0.2909]
[-0.0631 -0.2376]
[-0.3794 -0.0867]
[-0.3355 0.586 ]]
Projecting samples onto the new feature space
类似的,利用转换矩阵将训练数据投影到新的特征子空间上:1
2
3
4
5
6
7
8
9
10
11X_train_lda = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_lda[y_train==l, 0],
X_train_lda[y_train==l, 1],
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='upper right')
plt.show()
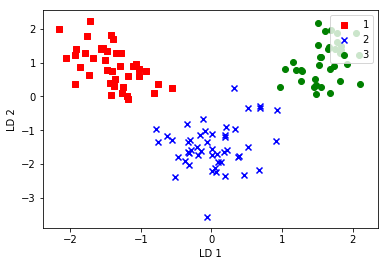
LDA via scikit-learn
逐步实现能够帮助我们理解LDA和PCA的内部实现差异,下面我们来看看scikit-learn自带的LDA类对数据降维,然后用逻辑回归来建模的效果;1
2
3
4
5
6
7
8
9
10
11X_train_lda = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_lda[y_train==l, 0],
X_train_lda[y_train==l, 1],
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='upper right')
plt.show()
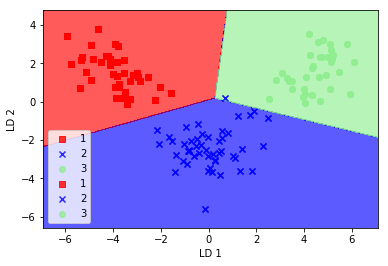
可以看到逻辑回归只有在一个样本上分类错误。但是通过降低正则化强度,我们能够适当调整分类面使得模型能够对所有数据正确分类。不过,我们先来看下模型在测试数据集上的表现情况:1
2
3
4
5
6X_test_lda = lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.show()
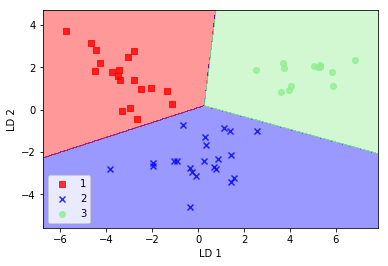
Bingo! 模型在测试集上100%正确,仅仅使用了2个特征向量而不是原始13个特征。
Using Kernel principal component analysis for nonlinear mappings
我们之前学习到的大部分机器学习算法都假设输入数据是线性分离的,而现实中我们可能遇到的更多的是非线性分类问题,此时类似PCA和LDA等线性转换技术来降维就不是一个好的选择。本节我们来看下核主成分分析(kernel PCA),将非线性分割问题转换到一个可以线性分类的低维子空间上。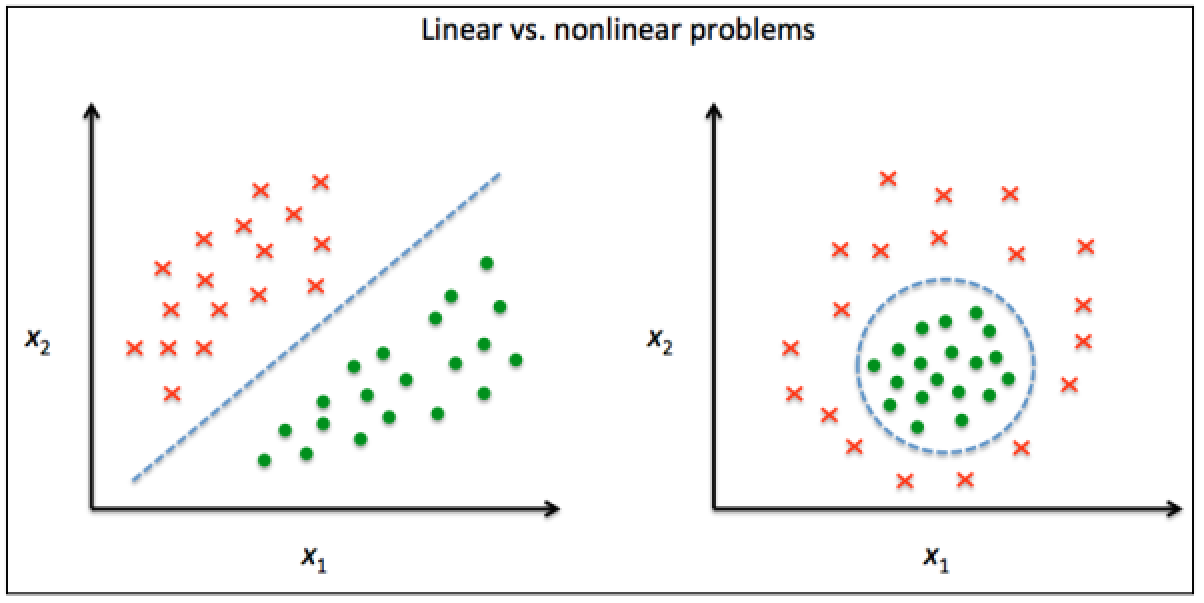
Kernel functions and the kernel trick
还记得我们在第三章介绍的核支持向量机,可以将非线性问题投射到更高维的线性空间上使其转化为线性可分。为了将样本数据转换到更高维的k维子空间上,我们定义了一个非线性映射函数Φ: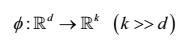
例如,如果x是一个二维向量,那么下面就是一种将它投射到三位空间上的一个方法: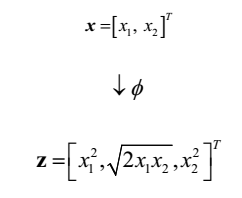
结合PCA,我们可以先把一个非线性可分的数据集投射到高维空间上,然后再通过PCA降维到另一个可线性分割的子空间上。这里的难点是,计算非常大,因此我们引入了核机制(kernel trick)。使用核机制可以在原有特征空间上计算两个高位特征向量间的相似度(similarity)。
主要是用到的和函数如下:
- 多项式核函数(the polynomial kernel)
- 双曲正切函数(the hyperbolic tangent)
- 高斯和函数或称为径向基函数(Gaussian kernel or Radial Basis Fucntion , RBF)
Implementing a kernel principal component analysis in Python
略
Projecting new data points
略
Kernelprincipal components analysis in scikit-learn
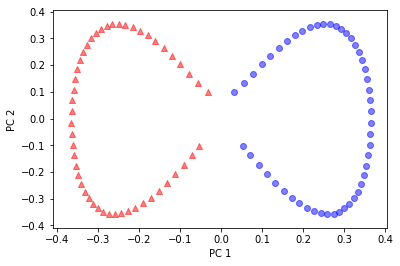
scikit-learn在sklearn.decomposion模块中实现了一个核PCA类,使用方法类似标准PCA类,我们可以通过参数kernel自定义和函数:1
2
3
4
5
6
7
8
9
10
11from sklearn.datasets import make_moons
from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples=100, random_state=123)
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()