Python Machine Learning III - Master Gloomymoon's R2D2

3 A Tour of Machine Learning Classifiers Using Scikit-learn

本章将浏览一系列流行而且强大的机器学习算法，学习区别的时候也会了解各个分类算法的强项和弱点。

流行分类算法的概要介绍
使用scikit-learn
选择一个机器学习算法前需要回答的问题

Choosing a classification algorithm

为特定任务选择合适的分类算法需要实践，每个算法都有各自的特性和前提假设，没有一个算法适用于所有场景。实践中，应当比较多个不同算法的效果来找到最合适的分类算法。请记住分类器的性能和预测能力主要依赖于（分析人员）对训练数据的理解。

训练算法的主要过程如下：

选择特征变量
选择性能评价指标
选择一个分类算法并优化（optimization）
评估模型的效果
算法调优（tuning）

First steps with scikit-learn

Training a perceptron via scikit-learn
我们先使用scikit-learn来训练一个感知器模型，训练数据仍使用Iris。

from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, [2,3]]
y = iris.target

因为使用频繁，iris已经被直接纳入scikit-learn包中，实际应用中也会用该数据来进行模型调试。和原始数据不同，这里的iris数据中的target已经转换成整型（0, 1, 2）,这也是算法调优推荐的做法。为了评估模型在未知数据上的性能，后续章节（第5章）会介绍如何将数据分为多个独立的部分，这里先了解主要用法。

1 2	from sklearn.cross_validation import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

使用train_test_split方法将X和y分成测试集（30%）和训练集（70%）。

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

StandardScaler对象的fit参数计算训练样本中每个特征维度的均值和标准差，transform方法则会根据均值和标准差对数据集进行标准化，注意这里对测试集和训练集使用的是同一个尺度（scaling）。

1
2
3

from sklearn.linear_model import Perceptron
ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)
ppn.fit(X_train_std, y_train)

Scikit-learn中的感知器用法和我们第二章中实现的类似，eta0等同于我们的eta，注意这里我们直接用三个分类的数据训练模型，之后就可以通过predict方法在测试集上进行预测。

1 2	y_pred = ppn.predict(X_test_std) print('Misclassfified samples: %d' % (y_test != y_pred).sum())

Output:

1	Misclassfified samples: 4

预测错误4个，错误率约等于8.9%（4/45）
Scikit-learn的metrics包中提供了各种不同的性能指标，例如准确率：

1 2	from sklearn.metrics import accuracy_score print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))

Output:

1	Accuracy: 0.91

最后我们可以使用第2章中编写的plot_decision_regions方法来展示模型分类效果，做的修改是为了高亮显示样本集数据。
Plot_decision_regions.py

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np

def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), 
    					   np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # plot all samples
    X_test, y_test = X[test_idx, :], y[test_idx]
    for idx, cl in enumerate(np.unique(y)):
    	plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
    				alpha=0.8, c=cmap(idx),
    				marker=markers[idx], label=cl)

    # highlight test samples
    if test_idx:
    	X_test, y_test = X[test_idx, :], y[test_idx]
    	plt.scatter(X_test[:, 0], X_test[:, 1], c='',
    				alpha=1.0, linewidth=1, marker='o',
    				s=55, label='test set')

展示感知器分类结果：

from plot_decision_regions import *
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std, y=y_combined, classifier=ppn, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

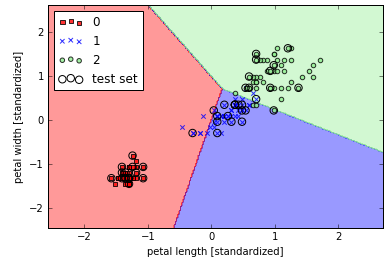
结果如图所示，对于无法线性区分的数据，感知器永远不会收敛。

Modeling class probabilities via logistic regression

感知器方法简单易懂，是很好的入门算法，但是因为存在上述缺陷无法有效应付类似的业务场景。我们来尝试另一个同样简单但是强大的分类器算法：逻辑回归，请注意其本质是一个线性/二元分类模型，而不是回归。
Logistic regression intuition and conditional probabilities
逻辑回归实现简单但是性能优秀，有广泛的应用。介绍逻辑回归这一概率模型前，先要引入比值比（odds radio，OR），其定义如下： p/(1-p)，其中p代表某个需要预测的事件出现的概率。在此基础上定义logit函数：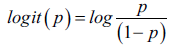

该函数输入洁玉0～1之间，输出是整个实数范围。因为我们更关心的是概率p的预测，所以需要需要对logit函数取反，就是logstic函数：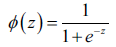

其中z是输入网络，是所有特征和权重的线性组合。因为该函数形如S，所以也成为sigmoid函数。下图是sigmoid在[-7, 7]范围上的曲线图：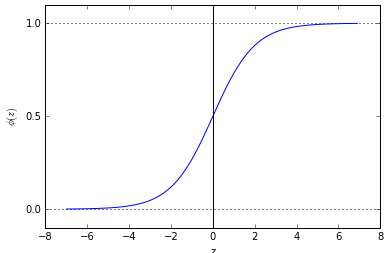

将之前我们实现的Adaline算法中的激活函数替换成sigmoid函数就成为了逻辑回归。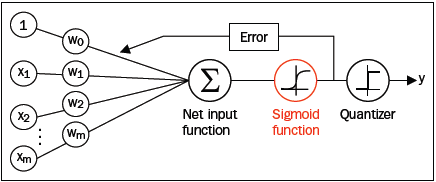

此时sigmoid函数的输出解释为样本数据属于分类1的概率。通过单步阶梯函数能够方便的转化为二元分类器，但是有的时候概率能够应用于更多的场景，例如降水概率、患病概率。

Learning the weights of the logistic cost function
（理论公式，略过）
Training a logistic regression model with scikit-learn

from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1000.0, random_state=0)
lr.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

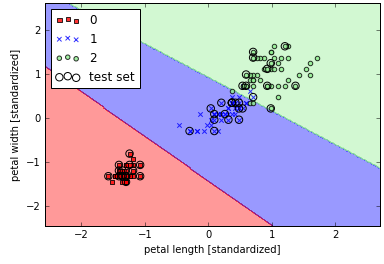
Scikit-learn实现了高效的逻辑回归算法，使用方法类似，训练后展示的分类效果如下图：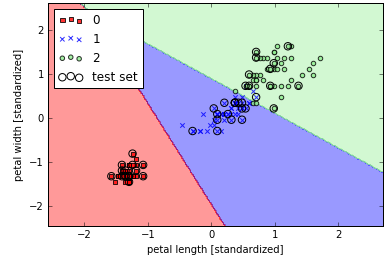

更进一步，我们能够预测单个样本划分到每类结果的概率：

1	lr.predict_proba(X_test_std[0, :])

Output:

1	array([[ 2.05743774e-11, 6.31620264e-02, 9.36837974e-01]])

Tackling overfitting via reqularization
在解释参数C以前，我们先了解下过拟合（overfitting）和正则化（regularization）。过拟合是指模型在训练集上表现良好但是在测试集上效果不佳（称作高方差，variance），可能是变量太多函数泰国复杂或者训练数据不够；也可能出现欠拟合（underfitting，也称作高偏差，bias）），模型没有很好的找到数据中的模式和规律，训练不足。下图虽然使用非线性分类边界描绘，但是能够直观地解释过拟合和欠拟合的情况和原因：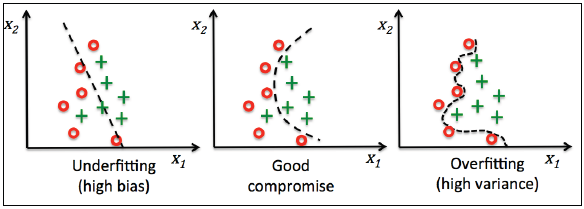

寻找合适的模型偏差-方差的一个方法是通过正则化调整模型的复杂程度。正则化能够有效应对变量同线性问题，过滤噪点数据，避免过拟合，其原理是对过度的权重参数进入额外的惩罚。最常用的正则化形式是L2正则化：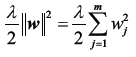

将这个结果加入到成本函数中，其中λ是正则化参数，λ越大正则化效应越大。

正则化也是将特征变量标准化的原因之一。

在scikit-learn实现中，参数C定义为λ的倒数，借用SVM的约定。降低C就是增加λ。

weights, params = [], []
for c in np.arange(-5, 5):
    lr = LogisticRegression(C=10**c, random_state=0)
    lr.fit(X_train_std, y_train)
    weights.append(lr.coef_[1])
    params.append(10**c)
weights = np.array(weights)
plt.plot(params, weights[:, 0], label='petal length')
plt.plot(params, weights[:, 1], linestyle='--', label='petal width')
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
plt.show()

从图上可以看出，当C变小时，特征变量的系统系数逐渐收缩到0，达到了正则化效应增强的结果。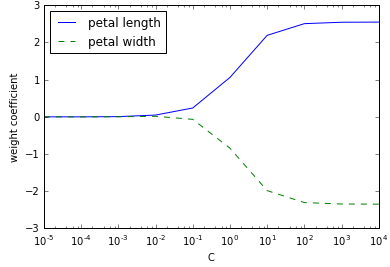

Maximum margin classification with support vector machines

另一个广泛使用的强大分类算法是支持向量机（support vector machine，SVM），其可以视为是感知器的延伸。在感知器算法中我们需要最小化错分类偏差，在支持向量机中优化目标是最大化类间间隔。类间间隔的定义是两个超平面之间的距离，训练集中最接近超平面的样本成为支持向量。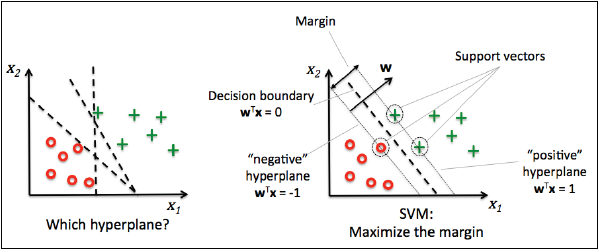

Maximum margin intuition
（计算公式推导，略过）

Dealing with the nonlinearly separable case using slack variables
这里不过分深入公式的推导，简单介绍下参数C的作用，如下图所示，通过参数C可以控制对错误分类结果的惩罚力度。C越大对错误分类的惩罚越大（即分类更加准确），C越小对错误分类的限制要求更宽松。因此C参数与正则化相关，通过增加C的大小，就会增加模型的偏度，降低模型的方差，这个影响关系和逻辑回归中的参数C的效用一致。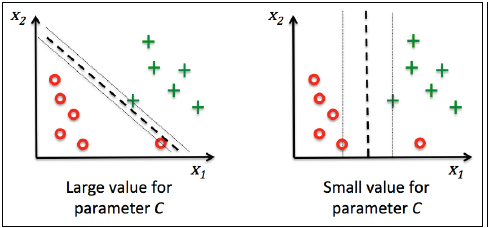

from sklearn.svm import SVC
svm = SVC(kernel='linear', C=1.0, random_state=0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

逻辑回归和支持向量机的比较
在实际分类问题中，线性逻辑回归和线性支持向量机的效果非常接近。两者的区别是，逻辑回归会尽可能利用所有数据，相较支持向量机会夸大异常点数据；而支持向量机更关注距离分类面最近的数据点（支持向量）。但是另一方面，逻辑回归的优势是实现相对简单，并且可以基于流数据在线更新。

Alternative implementations in scikit-learn
我们之前使用的模型底层调用的是优化后的C/C++库，另外，scikit-learn提供了另一种算法实现用于当训练数据太大无法装入内存的场景，原理类似于我们之前学习的Adaline的SGD实现方式，通过partial_fit方法来增量训练模型，调用方式如下：

from sklearn.linear_model import SGDClassifier
ppn = SGDClassifier(loss=’perceptron’)
lr = SGDClassifier(loss=’log’)
svm = SGDClassifier(loss=’hinge’)

Solving nonlinear problems using a kernel SVM

支持向量机广泛流行的另一个原因是能够容易地核化（kernelized）解决非线性分类问题。再讨论核函数支持向量机（kernel SVM）前，先来定义一个非线性分类的数据。
下面的代码使用logical_xor函数创建一个异或门形式的数据，其中100标记为1，100标记为-1。

np.random.seed(0)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] >0)
y_xor = np.where(y_xor, 1, -1)

plt.scatter(X_xor[y_xor==1, 0], X_xor[y_xor==1, 1], c='b', marker='x', label='1')
plt.scatter(X_xor[y_xor==-1, 0], X_xor[y_xor==-1, 1], c='r', marker='s', label='-1')
plt.ylim(-3.0)
plt.legend()
plt.show()

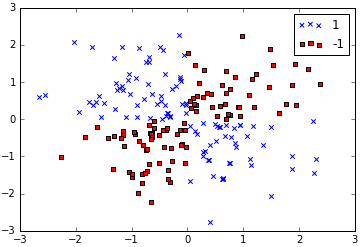
显然无法通过逻辑回归或线性SVM线性分割样本数据中的1和-1。这就需要用到核函数的基本思想：创建一个原始特征的非线性组合，将样本映射到高维空间，使他们成为线性可分割的。这里我们引入一个新的维度（即特征组合）：z3=x1^2+x2^2：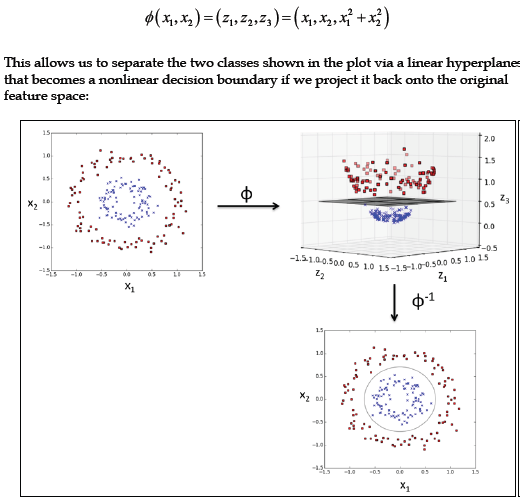

Using the kernel trick to find separating hyperplanes in higher dimensional space
使用最广泛的一个核函数是径向基函数（Radial Basis Function，RBF）或称作高斯核函数（Gaussian kernel），简化形式如下：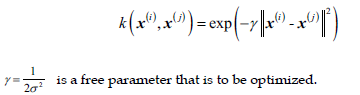

粗略地说，术语“核”可以简单理解为一对样本数据间的相似性函数（similarity function）。方程中的负号导致结果是越相似的样本返回越接近1，越不相似越接近0。现在我们就可以用之前的SVC类来训练非线性分类模型，简单的将参数kernel的值替换为’rbf’：

from sklearn.svm import SVC
svm = SVC(kernel='rbf', C=10.0, gamma=0.10, random_state=0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.show()

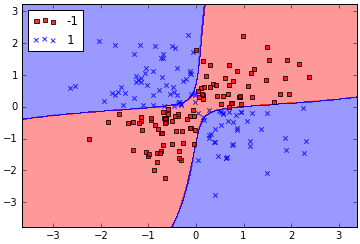
参数γ（程序中的gamma=0.1），可以理解为是高斯球面的切分点（cut-off）。如果增大参数γ，就会强化训练集数据的作用，结果就是导致更加拟合的分界面。为了直观理解，我们用iris数据训练RBF核函数支持向量机。

svm = SVC(kernel='rbf', random_state=0, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

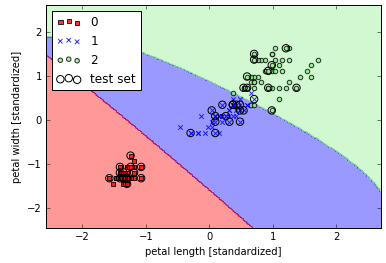
增加γ的取值后对比如下，注意观测分类边界：

svm = SVC(kernel='rbf', random_state=0, gamma=100.0, C=1.0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

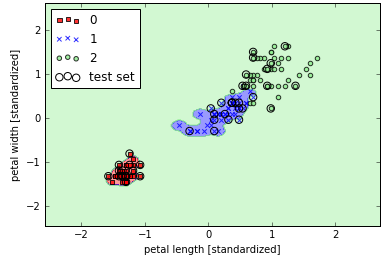
这次可以看出分类0和1的边紧贴样本数据，但是显然在未来新数据上会出现较高的正则化错误，可见参数γ在过拟合中具有显著影响。

Decision tree learning

决策树（decision tree）分类模型具有很好的可解释性，正如同其命名，决策树通过一系列问题并作出决策达到划分测试数据的目的。
决策树算法从根节点开始将数据按照特征基于信息增量（information gain）原则进行划分，然后对每个划分后的子集递归使用该方法，知道最终每个叶子数集只含有一个分类。实际中，严格按照这个原则会产生一个含有大量节点的深层次的过拟合决策树，所以，我们需要通过设置最大深度来对树进行剪枝。

Maximizing information gain – getting the most bang for the buck
首先定义决策树算法中需要优化的目标函数，这里目标函数的目标是最大化每次划分的信息增量值：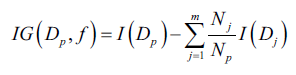

其中f是特征变量，Dp和Dj是划分前的父节点数据集和划分后的第j个子集，Np和Nj是父集和第j个子集的样本数，I是杂质度度量函数。简单来说信息增量就是划分后自己的杂质度总和-划分前的杂质度，划分后子集越纯信息增量越大。基于简单和复杂度因素考虑，很多库提供的都是二元决策树算法。
比较常用的三个杂质度量函数是基尼系数（Gini index）、信息熵（entropy）和分类错误（classification error）。
信息熵的定义如下：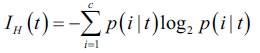

其中p标识样本中属于分类c的数量占比，当所有节点中的数据都属于同一类中时，信息熵为0。
基尼系数可以视为最小化误分类概率的判别准则：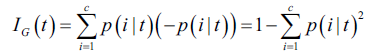

实践中基尼系数和信息熵的效果非常接近，无需刻意选择算法，不如测试不同的剪枝阈值。

另一个杂质度度量函数是分类错误：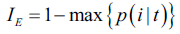

这是一个对剪枝较有用的衡量方法（而不是生成决策树）。下图展示的是不同杂质度和p分布情况下不同算法的差异：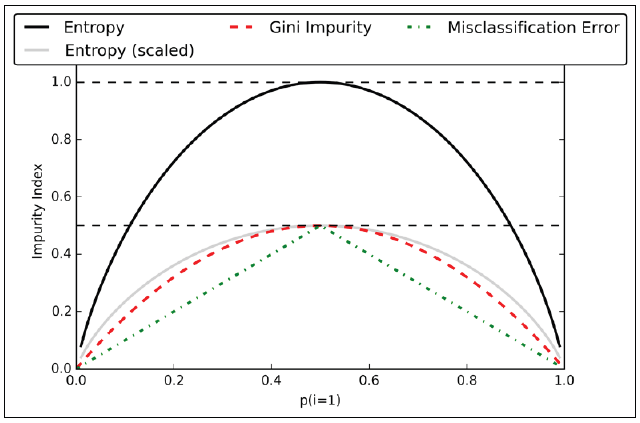

Building a decision tree
决策树会将特征空间切分为复杂的矩形，但是必须小心决策树的深度，因为更深的决策分支会形成更加复杂的切分矩形，也更容易产生过拟合。对决策树算法本身来说，特征变量归一不是必需的。

from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=0)
tree.fit(X_train, y_train)
X_combined = np.vstack((X_train, X_test))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X_combined, y_combined, classifier=tree, test_idx=range(105, 150))
plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.show()

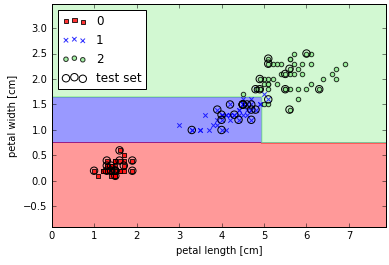
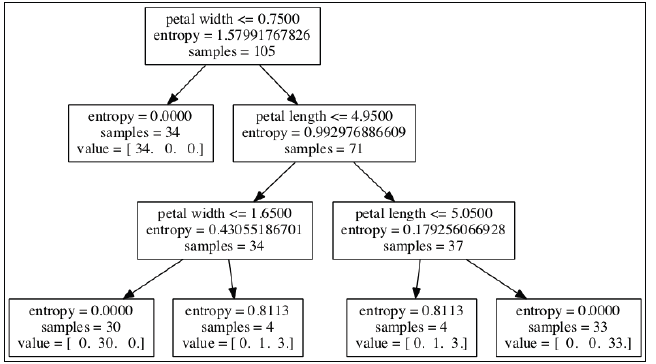
scikit-learn可以将生成的决策树导出为.dot文件，然后通过GraphViz程序做可视化展现。GraphViz程序可以在(www.graphviz.org)[http://www.graphviz.org]免费下载，提供Linux、Window和Mac OSX版本。

1 2	from sklearn.tree import export_graphviz export_graphviz(tree, out_file=’tree.dot’, feature_names=[‘petal length’, ‘petal width’])

安装完GraphViz后可以通过命令行将.dot文件输出为PNG图片：

1	dot –Tpng tree.dot –o tree.png

Combining weak to strong learners via random forests
随机森林（random forests）在近十年机器学习应用中广受欢迎，源于其优秀的性能、可扩展性和易使用性。随机森林可以直观地理解为是许多决策树的集合（ensemble），通过将许多弱分类器构建一个更加健壮的强分类器，可以有效降低正则化错误和过拟合。随机森林算法可以概括为以下四个步骤：

随机抽取数量为n的引导样本数据（从训练集中有放回的随机选择n个样本）；
基于引导样本生成一颗决策树。生成时遵循如下规则：无放回地随机选取d个特征变量，根据选定的d个特征变量选择最佳的切分方案，最佳的衡量可以采用例如信息增量最大的目标函数；
重复步骤1、2共k次；
根据预测结果按照多数投票算法（majority vote）整和所有的决策树。多数投票算法后续会详细介绍。

尽管随机森林无法提供像决策树这样清晰的可解释性，但是其巨大的优势在于：无需调优超变量、无需考虑剪枝问题、无需担心噪点数据的影响。我们只需要关注一个参数：树的棵数k。通常来说树越多，模型效果越好同时需要计算的时间也越多。
尽管如此，随机森林仍有超参数可以调优：引导样本的数量n和随机特征变量的数量d。样本数量n用于调节随机森林的偏度和方差，增大n数会降低样本的随机性，可能会增加过拟合情况。大多数算法（包括scikit-learn的RandomForestClassifier）实现中，默认引导样本数等于训练集中的样本数，一般这是一个较好的偏度-方差平衡点。随机特征数d一般都小于训练集中的总特征数，一个合理的默认值是总特征数m的平方根。

from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(criterion='entropy', n_estimators=10, random_state=1, n_jobs=2)
forest.fit(X_train, y_train)
plot_decision_regions(X_combined, y_combined, classifier=forest, test_idx=range(105, 150))
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc='upper left')
plt.show()

上述代码训练了一个有10棵数的森林，n_estimators定义了数的棵数，使用信息熵来衡量杂质度。n_jobs参数表示利用多核技术并行训练我们的模型，这里我们使用2个内核。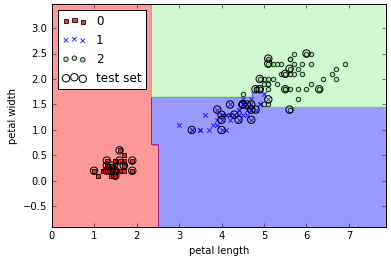

K-nearest neighbors – a lazy learning algorithm

最后本章讨论的是K近邻分类器（k-nearest neighbor，KNN），与之前介绍的算法不同，KNN是一种惰性学习（lazy learner），它不是在训练及上学习一个辨识函数，而是记忆训练集。

参数和非参数模型（Parametric versus nonparametric models）
机器学习算法可以简单分为参数和非参数模型。通过参数模型可以在训练及上学习一个含有参数的函数，可以用来对新数据分类。典型的如感知器、逻辑回归、线性SVM。而非参数模型无法特征化一系列参数，并且参数的个数会随着训练集变化。决策树和核函数SVM就是这类典型。
KNN属于非参数模型的一个子类，称为基于实例的学习（instance-based learning）。惰性学习是其中一种特殊情况，其学习过程没有任何成本（no cost）

KNN算法本身非常直观，可以概括为下述几步：

选取参数k和距离指标
选择距离待分类样本最近的k个邻居
根据多数投票算法对样本进行分类

下图展示了新数据（？点）是如何根据最近的5个邻居按照多数投票算法被分为三角形一类的过程。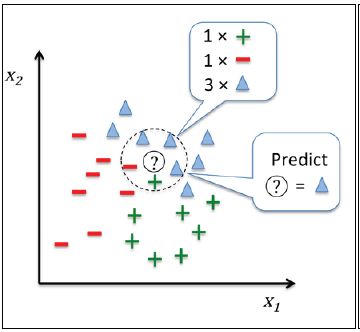

该类基于记忆的分类器一大优势是能够快速适应新的训练数据集，但是不利是最坏场景下算法复杂程度会随着样本数据增加线性增长，而且模型需要保存大量的样本数据，工作在大数据集上对存储空间也是一个挑战。
下面是使用欧几里德距离公式实现的KNN模型的代码：

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski')
knn.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=knn, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

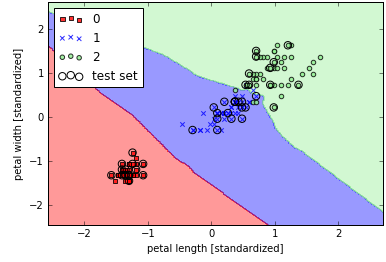
参数k的选择对于过拟合和欠拟合有着决定性的影响，同时还要注意距离计算公式能够适应数据的特性。欧式距离简单，并且通常适合于实数类型的特征值，如果使用欧式距离归一化也是必不可少的，这样可以保证所有的特征对距离的贡献平等。代码中的’minkowski’表示使用泛化（generalization）后的欧式距离或曼哈顿距离，参数p=2表示欧式距离，p=1表示曼哈顿距离。其他距离参数可以参考scikit-learn官网说明文档(sklearn.neighbors.DistanceMetric.html)[ http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html]。

维数灾难（The curse of dimensionality）
KNN很容易受到维数灾难影响产生过拟合。该影响可以简述为当特征维数很高但是样本数量不足造成所有的近邻距离都非常遥远。之前介绍的正则化无法应用于决策树和KNN，所以我们需要使用特征选择和降维技术来避免维数灾难。

3 A Tour of Machine Learning Classifiers Using Scikit-learn

Choosing a classification algorithm

First steps with scikit-learn

Modeling class probabilities via logistic regression

Maximum margin classification with support vector machines

Solving nonlinear problems using a kernel SVM

Decision tree learning

K-nearest neighbors – a lazy learning algorithm

FEATURED TAGS